一种受热力学启发的基于 AI 的搜索算法，用于求解常微分方程

快速阅读: 据《Nature.com》称，本文介绍了一种基于热力学原理的新型算法TSA，用于求解各类常微分方程。与传统方法相比，TSA表现出更高的准确性和鲁棒性，且无需依赖网格。实验验证其在初值和边值问题中均优于现有算法。

求解常微分方程（常微分方程）的问题是物理学、生物学、控制系统以及经济学等诸多科学与工程领域的关键且具有挑战性的计算难题。然而，传统数值方法，例如欧拉法和龙格-库塔法，通常面临网格依赖性、误差累积等问题，并非所有方法都适用于非线性和复杂系统。相反，元启发式算法成为一种颇具潜力的替代方案，将求解过程转化为优化任务。

本文提出了一种名为热力学启发式搜索算法（TSA）的新算法，用于近似求解线性常微分方程（LODEs）、非线性常微分方程（NLODEs）以及常微分方程组（SODEs）。受热力学过程、热交换、能量最小化和熵控制的启发，TSA 借助热力学原理，在搜索过程中实现全局探索与局部开发的平衡。通过结合傅里叶周期展开基函数、所提出的算法以及加权残差最小化方法，构建了一个无网格的常微分方程求解器，以精准逼近实际的常微分方程。

TSA 的种群是一组候选解，代表傅里叶展开级数的系数。它根据与适应度值相关联的能量来确定能量水平，通过解决方案之间的能量交换实现自适应探索。熵作为多样性的一种衡量标准，通过促进解的多样性防止过早收敛。通过逐步降温过程，探索向开发的转变逐渐完成。该问题被建模为带有约束条件的优化目标函数，其中常微分方程和边界条件的残差作为目标函数，惩罚函数确保约束满足。

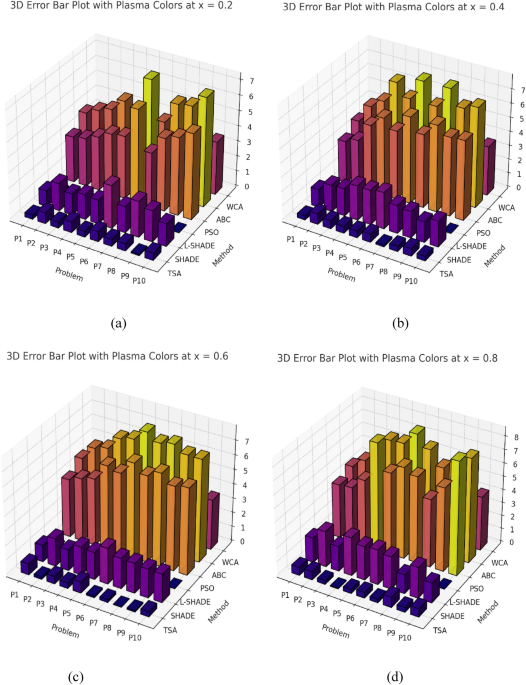
对TSA 在二十个常微分方程基准测试集上的进一步评估表明，其在准确性、收敛速度和鲁棒性方面优于最先进的常微分方程优化器，如ADE、PSO 和ABC。TSA 的无网格特性赋予了以下优势：(i) 不依赖网格；(ii) 使用熵保持多样性；(iii) 能量驱动的解更新。实验结果显示，TSA 在初值问题（IVPs）和边值问题（BVPs）中的均方根误差（RMSE）均低于现有算法。傅里叶周期展开和最小二乘加权残差方法提升了TSA 性能的近似精度。

所提算法为解决复杂常微分方程框架提供了稳健且灵活的设计框架，并可用于研究偏微分方程，探索局部-全局混合优化策略。

(以上内容均由Ai生成)