通过离线强化学习实现具有协同设计机制的交互式符号回归

快速阅读: 据《Nature.com》最新报道，研究提出Sym-Q算法，通过序列决策和协同优化机制，显著提升符号回归的泛化能力和效率，尤其适用于非分布内方程结构。与现有模型相比，Sym-Q在多个基准数据集上表现出色，并能有效整合专家知识，适用于更复杂方程及更高维场景，未来可进一步扩展和优化。

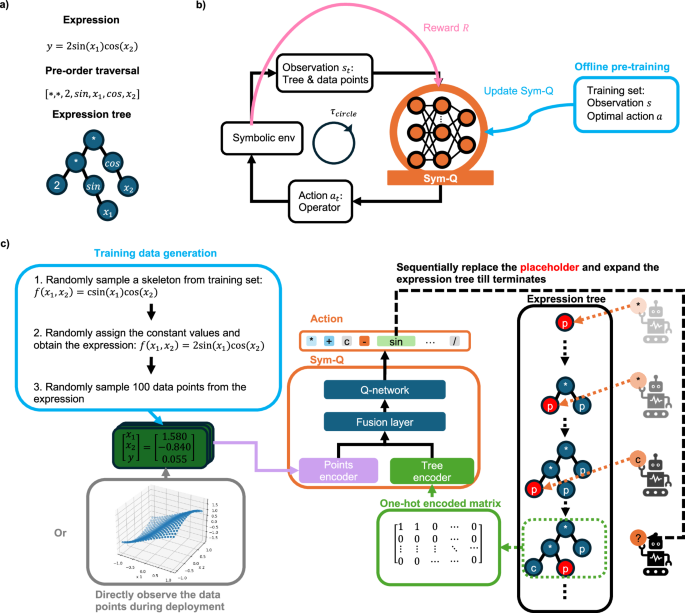
这项研究提出了一种先进的大规模符号回归范式，通过明确将其构建为一个序列决策任务，并采用提出的Sym-Q算法来解决。Sym-Q不仅擅长从零开始发现符号表达式，还克服了传统符号回归模型的一个关键局限性：由于有限的泛化和外推能力，它们在整合人类先验知识时效果较差且效率较低，尤其是在面对非分布内方程结构时。为了解决这一挑战，Sym-Q集成了一个协同优化机制，使表达式的交互式细化更加高效。这种创新方法允许领域专家提供部分定义的表达树，促进与模型的实时互动。通过动态修改生成的节点或提供先验信息，专家可以更有效地引导代理开发出精准捕捉潜在问题动态并符合已建立物理定律的数学表达式，特别是当部分领域知识可用时。这种协同优化机制有效地整合了专家见解和用户假设，提高了结果表达式的可解释性和科学相关性。

Sym-Q的关键优势之一在于其多功能性，它可以与各种类型的编码器结合使用，从先进的Transformer架构到更简单的RNN，用于处理表达树——从而区别于先前的研究。通过利用强化学习（RL），Sym-Q避免了暴露偏差，通过逐步引导模型构建方程。它不是记忆标记序列，而是基于观察动态生成表达式，显著减少了教师强制模型中固有的训练与测试不一致问题。这种结构化学习方法使Sym-Q能够更好地泛化并更有效地适应未见过的方程。

为了实现有意义且公正的评估，我们将Sym-Q与三种最先进的基于Transformer的监督学习模型进行了比较，这些模型像Sym-Q一样没有包含额外的在线搜索机制。广泛的基准评估表明，Sym-Q在大多数用于预训练大规模符号回归模型的基准数据集上与其他最先进的算法在拟合准确度和恢复率方面表现相当。这个创新框架特别适合协同设计，实验表明Sym-Q的协同优化机制行之有效。通过整合领域知识，Sym-Q有效处理复杂情况，如在费曼数据集中恢复漂移项以及从合成过境光谱中推导分析表达式。这种整合导致恢复率和决定系数均有显著提高。我们的实验表明，随着更多领域专业知识的融入，协同设计方法不仅提升了性能指标，还使模型输出与潜在的物理定律和模式保持一致。与NeSymReS相比，Sym-Q的协同优化机制始终展现出更可靠的改进，在不同程度的真实值可用性下有效利用了部分信息。

除了当前的性能提升，Sym-Q的协同设计能力推动了符号回归领域的重要进展，特别是在涉及非分布内方程结构的场景中。通过有效地利用部分先验知识并动态适应不熟悉的方程形式，Sym-Q展示了强大的泛化和适应能力，成为解决复杂现实世界问题的强大工具。

未来研究的一个有前景的方向是将Sym-Q扩展至处理更复杂的表达式类型，例如常微分方程和偏微分方程。此外，对协同优化框架的进一步改进可以探索更复杂的方式整合专家知识，可能包括综合约束条件或分层指引以进一步完善发现过程。虽然我们已经验证了Sym-Q从两个变量到三个变量的可扩展性，但将模型拓展至更高维度仍然是未来研究的重要方向。

(以上内容均由Ai生成)