使用整数加法进行近似浮点乘法

快速阅读: 据《黑客日》最新报道，整数方法在低精度需求场景下实用，但其效率未必优于浮点运算。将GPU的高效浮点处理能力转移至CPU是否节能增效，仍需验证。

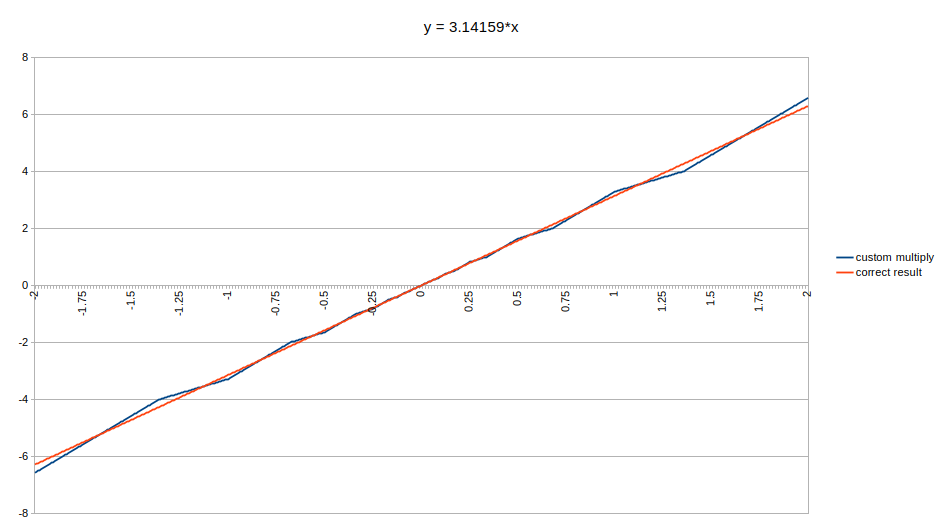
曾经深奥的科学与商业计算领域中的浮点运算，如今已渗透至生活的方方面面。从电子游戏到大型语言模型，缺乏浮点运算能力的处理器几乎难以立足。然而，现实是基于整数的近似值已足够满足所需精度。例如，马尔特·斯卡鲁克近期提到的香港洛和孙伟提出的大型语言模型方法，正是以整数加法为基础。这种方法乍看之下就是字面意思：将两个浮点输入视作整数值相加，随后调整指数。这一调整因子虽能接近正确答案，但正如文章及其评论所示，你必须面对诸多问题和特殊情况。这些问题包括溢出与下溢，也涉及特定的浮点输入。与科学计算不同，图形渲染和大型语言模型对浮点精度的要求并不苛刻，因此整数方法7.5%左右的准确率已足够实用。

问题是，这种整数方法真的比论文所暗示的更高效吗？抑或只是如某些仅靠整数运算的音频解码器那般，是一种折衷方案，例如在没有浮点处理器（FPU）的平台上运行。毕竟，像GPU及其变种这样专注于浮点运算的向量处理器的一大优势，就在于能够高效处理海量数据。因此，试图将这种功能转移到CPU的算术逻辑单元上，并期待显著节能提升，似乎显得过于乐观。毕竟，将这种高效的数据处理能力移植到CPU上，能否真正实现性能飞跃，还有待观察。

(以上内容均由Ai生成)