灵活且经济高效的深度学习，用于使用相位循环 bSSFP 加速多参数弛豫测量

快速阅读: 据《Nature.com》最新报道，PINNs架构的参数值边界由开发者预设，限制了其外推能力。对于\(T_1\)和\(T_2\)、\(\Delta B_0\)和\(B_1^+\)等参数，若超出预设范围，则需重新训练模型。例如，\(\Delta B_0\)的训练样本覆盖了\(\theta\)的\(2\pi\)范围，而\(B_1^+\)的准确估计仅在0.7到1.3范围内有效。这意味着模型在不同参数范围下的表现会有所不同，需要特定的处理方法来确保准确性。

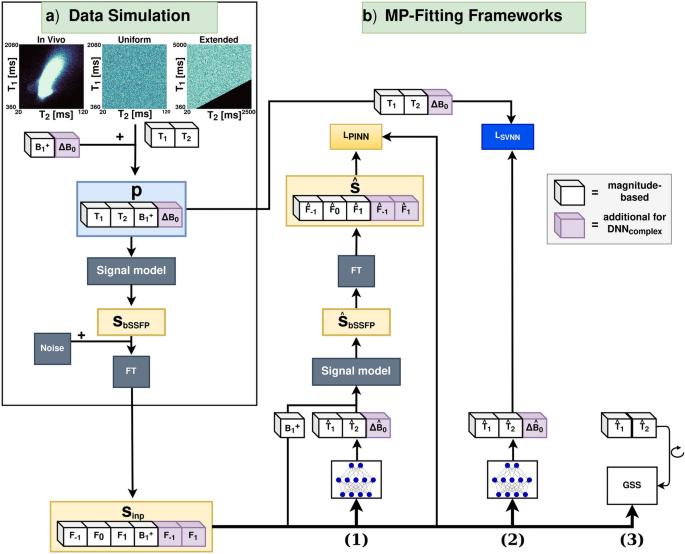
PINNs架构固有的参数值边界是可实现的，并且这些边界是由开发者预定义的，禁止外推。因此，PINNs的一个局限性在于，如果感兴趣的参数范围超出模拟范围，则需要重新训练。这不仅限于\(T_1\)和\(T_2\)值的范围，也适用于\(\Delta B_0\)和\(B_1^+\)分布。对于\(\Delta B_0\)，基于复杂数据的深度神经网络（DNNs）训练样本主要覆盖了与失谐相关的相位累积（\(\theta\)）的\(2\pi\)范围，排除了\(\pm \pi\)边界以帮助复杂数据DNNs更好地收敛。由于复数值\(F_n\)模式的信号在去除了相位循环维度上的常量相位偏移后，在\(\theta\)中表现出\(2\pi\)周期性，因此，\(\theta\)的模拟范围足以确保即使超出\(2\pi\)范围，\(\Delta B_0\)的\(T_1\)和\(T_2\)估计依然可靠。如果要可靠地估计\(\Delta B_0\)（这并非本研究的目标），则需要采用解缠策略来处理\(2\pi\)相位包裹。

对于\(B_1^+\)，训练好的DNNs对\(B_1^+\)值在0.7到1.3范围内的准确松弛度值提供准确估计，这与体外训练数据的范围相对应（参见补充图S10）。然而，需要注意的是，性能依赖于外部\(B_1^+\)推导的准确性。如果测量值与实际\(B_1^+\)存在差异，那么\(T_1\)的估计结果可能会产生偏差。有趣的是，只要实际\(B_1^+\)值处于训练过的\(B_1^+\)值范围内，\(T_2\)的估计基本不受影响（参见补充图S10）——这种行为类似于MIRACLE 27的方法。

(以上内容均由Ai生成)